Affichage des articles dont le libellé est probabilités. Afficher tous les articles
Affichage des articles dont le libellé est probabilités. Afficher tous les articles
mardi 11 mai 2010
jeudi 6 mai 2010
lundi 3 mai 2010
Quatre amis se retrouvent dans quatre salles de cinéma...
Chaque ami choisit indépendamment des autres une salle de cinéma. L'univers de cette expérience aléatoire est composé de $4 \times 4 \times 4 \times 4=4^4=256$ quadruplets correspondant chacun aux choix respectifs des quatre amis.
Soit $A$ l'évènement: Ils se retrouvent dans des salles différentes.
En utilisant la méthode des cases de choix, on obtient 4 choix pour le premier ami, puis 3 pour le deuxième qui ne eput se trouver dans la même salle, puis 2 pour le troisièmes et enfin 1 pour le dernier.
Il y a donc $4 \times 3 \times 2 \times 1 = 24$ cas favorables.
Nous sommes en situation d'équiprobabilité, puisque les choix se font indépendamment les uns des autres, la probabilité d'un évènement s'obtient donc comme le quotient des cas favorables sur la totalité des cas possibles.
Il y a donc $4 \times 3 \times 2 \times 1 = 24$ cas favorables.
Nous sommes en situation d'équiprobabilité, puisque les choix se font indépendamment les uns des autres, la probabilité d'un évènement s'obtient donc comme le quotient des cas favorables sur la totalité des cas possibles.
$$p(A)=\frac{24}{256} = \frac{3}{32}$$
Soit $B$ l'évènement : Au moins deux se retrouvent dans la même salle.
On remarque que $$B= \overline{A}$$.
Ainsi:
$$p(B)=1-p(A)= \frac{29}{32}$$
On peut faire un dénombrement direct, mais cela n'est pas très adapté compte tenu de la simplicité du pasage par l'évènement contraire et le fait que l'évenment $B$ recouvre la quasi-totalité des issues possibles.
Il faut considérer 3 cas:
Deux amis exactement se rencontrent dans la même salle.
Et là il faut considérer deux sous-cas suivants que les deux amis restants se rencontrent ou non dans une même autre salle.
Deux amis se rencontrent dans une même salle et les deux autres dans deux salles différentes:
On fixe la salle et les amis soit : $1\times 1 \times 3 \times 2 $.
On multiplie par le nombre de salle possibles soit 4 et le nombre de positions (qui correspondent aux amis) de 2 éléments parmi 4 soit 6. On trouve donc 144 cas favorables.
Deux amis se rencontrent dans une même salle et les deux autre dans une même autre salle.
On fixe la salle et les amis soit $1 \times 1 \times 3 \times 1=3$ car le dernier ami doit aller dans la salle du troisième. Il n'a pas le choix, tout comme le deuxième.
On fait maintenant varier les salles, il y en a 4 possibles et les positions . Il faut cependant faire attention car il n'y en a plus 6 mais 3 car il existe des symétries. Il ne faut pas compter deux fois les issues.
On trouve donc 36 cas favorables.
Trois amis se retrouvent dans la même salle.
Avec le même procédé que précédemment on trouve : $1\times 1 \times 1 \times 3$ multtiplié par le nombre de salles, soit 4, puis le nombre de possibilité de faire le choix de trois élément parmi 4, d'ailleurs identique aux choix possibles d'un élément parmi 4, soit 4. On a donc 48 issues favorables.
Quatre amis se retrouvent dans la même salle. On trouve aisément qu'il n'y a que 4 issues favorables.
On trouve donc :
On remarque que $$B= \overline{A}$$.
Ainsi:
$$p(B)=1-p(A)= \frac{29}{32}$$
On peut faire un dénombrement direct, mais cela n'est pas très adapté compte tenu de la simplicité du pasage par l'évènement contraire et le fait que l'évenment $B$ recouvre la quasi-totalité des issues possibles.
Il faut considérer 3 cas:
Deux amis exactement se rencontrent dans la même salle.
Et là il faut considérer deux sous-cas suivants que les deux amis restants se rencontrent ou non dans une même autre salle.
Deux amis se rencontrent dans une même salle et les deux autres dans deux salles différentes:
On fixe la salle et les amis soit : $1\times 1 \times 3 \times 2 $.
On multiplie par le nombre de salle possibles soit 4 et le nombre de positions (qui correspondent aux amis) de 2 éléments parmi 4 soit 6. On trouve donc 144 cas favorables.
Deux amis se rencontrent dans une même salle et les deux autre dans une même autre salle.
On fixe la salle et les amis soit $1 \times 1 \times 3 \times 1=3$ car le dernier ami doit aller dans la salle du troisième. Il n'a pas le choix, tout comme le deuxième.
On fait maintenant varier les salles, il y en a 4 possibles et les positions . Il faut cependant faire attention car il n'y en a plus 6 mais 3 car il existe des symétries. Il ne faut pas compter deux fois les issues.
On trouve donc 36 cas favorables.
Trois amis se retrouvent dans la même salle.
Avec le même procédé que précédemment on trouve : $1\times 1 \times 1 \times 3$ multtiplié par le nombre de salles, soit 4, puis le nombre de possibilité de faire le choix de trois élément parmi 4, d'ailleurs identique aux choix possibles d'un élément parmi 4, soit 4. On a donc 48 issues favorables.
Quatre amis se retrouvent dans la même salle. On trouve aisément qu'il n'y a que 4 issues favorables.
On trouve donc :
$$p(B)= \frac{144+36+48+4}{256}=\frac{232}{256}=\frac{29}{32}$$
dimanche 4 avril 2010
lundi 29 mars 2010
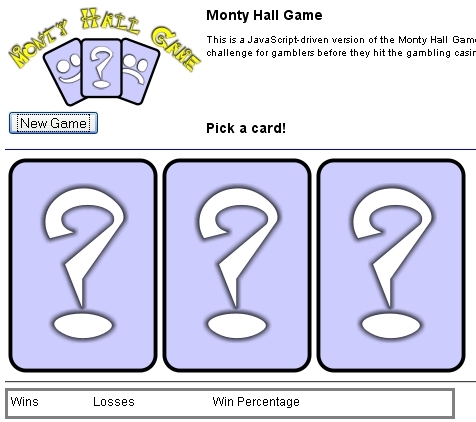
Le paradoxe de Monty Hall en probabilités conditionnelles
Qu'est-ce que le problème de Monty Hall ? Il est issu d'un jeu télévisé.
Il y a trois cartes devant vous faces cachées. L'une des trois est gagnante et vous devez la trouver.
Vous en choisissez une des trois sans la regarder.
Quelqu'un qui connait les cartes, en retourne, une des deux que vous n'avez pas choisie et qui est perdante.
Que devez vous faire? Retourner la carte que vous avez choisie initialement ou retourner l'autre ?
Les probabilités sont formelles, vous devez impérativement changer votre choix pour augmenter vos chances de gagner.
Essayez par vous même:
Il y a trois cartes devant vous faces cachées. L'une des trois est gagnante et vous devez la trouver.
Vous en choisissez une des trois sans la regarder.
Quelqu'un qui connait les cartes, en retourne, une des deux que vous n'avez pas choisie et qui est perdante.
Que devez vous faire? Retourner la carte que vous avez choisie initialement ou retourner l'autre ?
Les probabilités sont formelles, vous devez impérativement changer votre choix pour augmenter vos chances de gagner.
Essayez par vous même:
Les probabilités au coeur de la justice: l'affaire Sally Clarck
En 1996 , un couple d'Anglais Sally et Steve Clark ont le malheur de perdre leur fils Christopher de la mort subite du nourisson. 13 mois plus tard, leur second fils Harry décède lui aussi de la même façon.
Les parents sont alors soupçonnés d'avoir tué les deux enfants.
L'accusation s'appuie sur l'argument suivant: Dans une famille aisée, non fumeur, dont la mère a plus de 26 ans, la probabilité d'une mort subite du nourrisson est de 1/8543 donc la probabilités de deux morts subites du nourrisson est de (1/8543)x(1/8543) soit une chance sur... 73 millions !
La suite ICI
dimanche 28 mars 2010
dimanche 3 mai 2009
Les zanniversaires
dimanche 5 avril 2009
Dénombrements
Le Loto
Un article sympa accessible aux TS : Probabilités et Loto
1125899906842624 dessins
Un peu de dénombrement....
Avec 50 cases à cocher, affichant chacune un dessin ou un autre, vous pouvez réaliser exactement 250 jolis dessins. C'est ce que propose Wolfram ICI. ( Il faut installer le player Mathematicapour visualiser )
Sachant que vous allez regarder à peu près un dessin par seconde, combien de temps devrez-vous avoir devant vous pour les regarder tous ?
Impressionnant non ? Allez on se dépèche, et je suis d'accord pour repousser l'interro la semaine prochaine :)
Un article sympa accessible aux TS : Probabilités et Loto
En jouant toute votre vie, vous avez une chance sur 1 676 de gagner le gros lot donc mieux vaut bosser comme tout le monde et ne pas jouer au Loto. Cependant, les 8 348 tirages ont coûté « seulement » 5 000 euros et le retour sur investissement est donc bien meilleur par rapport à la bourse mais les chances de gagner sont nettement plus faibles !
Un peu de dénombrement....
Avec 50 cases à cocher, affichant chacune un dessin ou un autre, vous pouvez réaliser exactement 250 jolis dessins. C'est ce que propose Wolfram ICI. ( Il faut installer le player Mathematicapour visualiser )
Impressionnant non ? Allez on se dépèche, et je suis d'accord pour repousser l'interro la semaine prochaine :)
jeudi 15 janvier 2009
vendredi 13 juin 2008
mardi 10 juin 2008
Probabilités - Anniversaires - premières S
La probabilité que dans un groupe de 30, au moins deux personnes aient le même jour d'anniversaire est de:
soit environ 70%.
Pas de chance pour votre classe qui fait partie des 30% restant, par contre 2 élèves sont nés le même jour dans ma classe de seconde ainsi que dans ma classe de terminale ES.
Le paradoxe des anniversaires : ICI
soit environ 70%.Pas de chance pour votre classe qui fait partie des 30% restant, par contre 2 élèves sont nés le même jour dans ma classe de seconde ainsi que dans ma classe de terminale ES.
Le paradoxe des anniversaires : ICI
Inscription à :
Articles (Atom)
Articles
