Comportement asymptotique

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

Utilisez les curseurs pour modifier l'expression de $f$

Les sujets 2010 du bac Pondichery

ICI

Annales corrigées de Terminale ES

• Annales corrigées à partir de 2005

• Annales corrigées à partir de 2004

• Sujets d’annales corrigées interactifs

• Annales corrigées depuis 2001

• Tous les sujets depuis 1999 dont 2 corrigés
   
• Module de révisions XMaths
  
  

Maîtriser la compétence: " Etudier le signe d'une expression"

Bien souvent l'étude du signe d'une expression se réduit à le donner directement, sans aucune justification. Dans les cas les plus problématiques, ce signe n'est même pas validé par une étude à l'aide de la calculatrice. De la seconde à la terminale, l'étude du signe d'une expression simple, qui intervient la plupart du temps à partir de la première au travers de l'étude de la fonction dérivée pour en déduire les variations de la fonction, celle-ci est souvent négligée.Le tableau des variations est régulièrement posé comme par magie derrière le calcul de la dérivée. Parfois il est correct mais dans certains cas, la négligence conduit à l'erreur et ceci indépendamment de la difficulté lié à l'étude du signe.

Lors de l'étude du signe d'une fonction dérivée, l'inéquation  n'est pas posée, il faut donc l'écrire.
Parfois l'expression est à modifier ( souvent à factoriser mais pas toujours) et il faut dégager les différents blocs du quotient ou du produit afin d'étudier leur signe. Dans tous les cas, l'étude d'un signe complexe se ramène à plusieurs études simples. 

Le domaine d'étude de la fonction est quelquefois primordial et permet de conclure directement.

Dans l'idéal, toute étude de signe devrait être justifiée par des théorèmes ou des propriétés vues en cours ( somme de fonctions positives, second degré, règle des signes, utilisation des variations de la fonction, utilisation des variations d'une fonction de référence...)

Lorsque le domaine d'étude fait tout le travail

• Étude du signe de  $x+\frac{1}{x}$ sur $]0;+\infty [$

$x>0$ et $\frac{1}{x}>0$
La somme de deux expressions strictement positives est strictement positive, ainsi  $x+\frac{1}{x}>0$ sur $]0;+\infty [$


Un signe élémentaire et pourtant...

• Étude du signe de  $\frac{1}{5}\frac{4x-1}{x}$ sur $]0;+\infty [$

Cette question peut être abordée en seconde, mais lorsqu'il s'agit , par exemple, d'y répondre lors d'une étude de signe de dérivée en Terminale, elle peut s'avérer problématique.

$\frac{1}{5}>0$  et  $\\x>0$

Il faut résoudre l'inéquation $4x-1\geq 0$

soit $\color{red}x\geq \frac{1}{4}$

On peut ainsi dresser le tableau de signe suivant ( qu'il corresponde à celui d'une dérivée, une différence entre deux fonctions pour étudier les positions relatives des courbes, ou tout autre usage) :

Étudier le signe de $ \frac{1-ln(x+3)}{(x+3)^2^}$ pour $x>0$:

Effectivement, ça sent un peut le signe de dérivée, mais contrairement aux apparences trompeuses, les justifications attendues sont loin d'être toujours au rendez-vous!

Ce n'est pas le signe de $(x+3)^2$ qui pose problème mais plutôt celui de $1-ln(x+3)$
Résolvons pour cela l'inéquation suivante:
$1-ln(x+3)\geq 0$
$ 1\geq ln(x+3)$
$ ln(e)\geq ln(x+3)$
La justification attendue ici est que la fonction $ln$ est strictement croissante sur $\mathbb{R}^*_+$
$e\geq x+3$
$x\leq e-3<0$

Ainsi, pour tout $x>0$, $1-ln(x+3)<0$ et donc l'expression initiale aussi.

Entrainement aux techniques de base en Terminale ES

Equations de droites
Test en ligne
Associer une droite et sa représentation graphique
Associer des droites à leur expression ICI et ICI
Déterminer l’expression algébrique d’une fonction affine dont la représentation est donnée


Pourcentages
Evolutions successives
Suites et pourcentages


Limites
Limite à l’infini d’une fonction polynôme
Limite à l’infini d’une fonction rationnelle
Limite de 1/u


Dérivation
Exercices sur la dérivée (1ère)
Lecture graphique du nombre dérivé:  1 2 3 4 et 5
Déterminer graphiquement une équation de tangente
Signe de la dérivée / Variation de fonction
Reconnaître la courbe d’une fonction dérivée


Intégration
Encadrer une intégrale à l’aide de 2 entiers consécutifs
Reconnaître la courbe d’une primitive


Logarithme
Propriétés algébriques de la fonction ln: 1 et 2

Ensemble de définition de lnf où f est une fonction affine
Ensemble de définition d’une fonction du type lnf
Limite de lnu
Dérivée d’une fonction klnu
Associer des produits ou quotients de logarithmes de fonctions dérivable à leur dérivée
Primitives de ku’/u
Calcul d’une intégrale de ku’/u


Statistiques
Ajustement affine par la méthode des moindres carrés
Outil en ligne d’ajustement affine par la méthode des moindres carré


Exponentielle
Techniques de base

Diagrammes de Venn

Cliquer ICI

Fiches calculatrices

Les fiches de Xmaths : ICI

Calculatrices TI Le fichier PDF

Programmation

• Sur TI
• Sur Casio

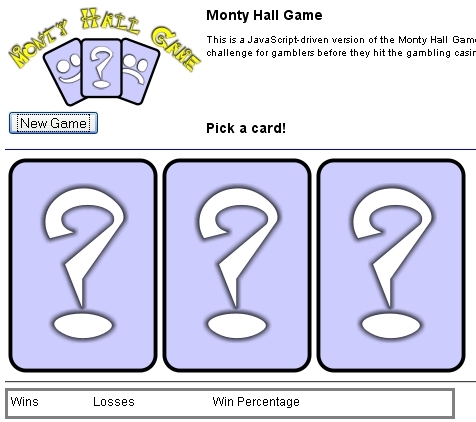
Le paradoxe de Monty Hall en probabilités conditionnelles

Qu'est-ce que le problème de Monty Hall ? Il est issu d'un jeu télévisé.

Il y a trois cartes devant vous faces cachées. L'une des trois est gagnante et vous devez la trouver.

Vous en choisissez une des trois sans la regarder.

Quelqu'un qui connait les cartes, en retourne, une des deux que vous n'avez pas choisie et qui est perdante.

Que devez vous faire? Retourner la carte que vous avez choisie initialement ou retourner l'autre ?

Les probabilités sont formelles, vous devez impérativement changer votre choix pour augmenter vos chances de gagner.

Essayez par vous même:

Les probabilités au coeur de la justice: l'affaire Sally Clarck

En 1996 , un couple d'Anglais Sally et Steve Clark ont le malheur de perdre leur fils Christopher de la mort subite du nourisson. 13 mois plus tard, leur second fils Harry décède lui aussi de la même façon.

Les parents sont alors soupçonnés d'avoir tué les deux enfants.

L'accusation s'appuie sur l'argument suivant: Dans une famille aisée, non fumeur, dont la mère a plus de 26 ans, la probabilité d'une mort subite du nourrisson est de 1/8543 donc la probabilités de deux morts subites du nourrisson est de (1/8543)x(1/8543) soit une chance sur... 73 millions !

La suite ICI

Point clé: Détermination de primitives par lecture inverse du tableau des dérivées

TELECHARGER -> Point clé détermination de primitives par lecture inverse du tableau de dérivées



Visualiser les courbes des fonctions dérivée et d'une primitive avec GeoGebra

Point clé: Inverser un arbre pondéré

Télécharger -> Inverser un arbre pondéré

Point clé: Lien entre dérivée, fonction et primitive

Télécharger -> Point clé lien entre f, f' et F



Visualiser les courbes des fonctions dérivée et d'une primitive avec GeoGebra

Point clé: lecture graphique d'un nombre dérivé

Télécharger -> Point clé lecture graphique du nombre dérivé

Point clé: Concrètement c'est quoi l'intégrale de a à b de f(x)dx quand f>0 ?

Télécharger -> Point clé intégrale

Point clé : quelques apparitions du nombre e

Télécharger -> Point clé quelques apparitions du nombre e

Point clé: Fonction ln : sympa -pas sympa

Télécharger -> Point clé fonction ln

Bien débuter avec l'exponentielle

Quelques adresses pour l'exponentielle on Prezi

entrainement exponentielle

ln et exp

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

Dénombrements

 Le Loto

Un article sympa accessible aux TS : Probabilités et Loto

En jouant toute votre vie, vous avez une chance sur 1 676 de gagner le gros lot donc mieux vaut bosser comme tout le monde et ne pas jouer au Loto. Cependant, les 8 348 tirages ont coûté « seulement » 5 000 euros et le retour sur investissement est donc bien meilleur par rapport à la bourse mais les chances de gagner sont nettement plus faibles ! 

1125899906842624 dessins


Un peu de dénombrement....

Avec 50 cases à cocher, affichant chacune un dessin ou un autre, vous pouvez réaliser exactement 2⁵⁰ jolis dessins. C'est ce que propose Wolfram ICI. ( Il faut installer le player Mathematicapour visualiser )

Sachant que vous allez regarder à peu près un dessin par seconde, combien de temps devrez-vous avoir devant vous pour les regarder tous ?
Impressionnant non ? Allez on se dépèche, et je suis d'accord pour repousser l'interro la semaine prochaine :)

Indice de développement humain et espérance de vie

Nous avons abordé en statistiques l'IDH et l'espérance de vie, voilà quelques compléments.

L'IDH est un indice composite, sans unité, compris entre 0 (exécrable) et 1 (excellent), calculé par la moyenne de trois indices quantifiant respectivement :

• la santé /longévité (mesurées par l'espérance de vie à la naissance), qui permet de mesurer indirectement la satisfaction des besoins matériels essentiels tels que l'accès à une alimentation saine, à l'eau potable, à un logement décent, à une bonne hygiène et aux soins médicaux. En 2002, la Division de la population des Nations Unies a pris en compte dans son estimation les impacts démographiques de l'épidémie du sida pour 53 pays, contre 45 en 2000.
• le savoir ou niveau d'éducation. Il est mesuré par le taux d'alphabétisation des adultes (pourcentage des 15 ans et plus sachant écrire et comprendre aisément un texte court et simple traitant de la vie quotidienne) et le taux brut de scolarisation (mesure combinée des taux pour le primaire, le secondaire et le supérieur). Il traduit la satisfaction des besoins immatériels tels que la capacité à participer aux prises de décision sur le lieu de travail ou dans la société ;
• le niveau de vie (logarithme du produit intérieur brut par habitant en parité de pouvoir d'achat), afin d'englober les éléments de la qualité de vie qui ne sont pas décrits par les deux premiers indices tels que la mobilité ou l'accès à la culture.

La suite de l'article de wikipédia : Indice de développement humain

Le classement IDH 2005 des pays

En ce qui concerne l'espérance de vie, je vous propose un article clarifiant cette notion difficile à saisir.
L’espérance de vie est un indice conjoncturel, ce n’est pas plus la prévision de l’âge moyen des décès de l’année que la durée de vie de ceux et celles qui viennent de naître !

L'article complet sur Images des mathématiques.